Uma Análise Epistemológica Sobre A Representação Dos Objetos Matemáticos

Ao longo da história da Matemática, povos e/ou estudiosos da área preocuparam-se em desenvolver representações cada vez mais sofisticadas para conceber um objeto matemático. Essas representações, por sua vez, foram modificadas, alteradas ou melhoradas inicialmente com o objetivo de sintetizar ou resolver problemas com maior otimização. Uma situação simples, para exemplificar, é a própria representação dos algarismos. É indiscutível que escrever e operar com algarismos arábicos é muito mais simples do que com algarismos romanos. A diferença significativa entre essas duas representações é justamente o fato da primeira existir uma representação para “o nada”, ou seja, o algarismo zero. Um dos fatos relevantes aqui é entender que foram circunstâncias históricas, uma das responsáveis pela concepção que se tem hoje do que é o número. As representações atuais não foram simplesmente pensadas do dia para noite.

 

A idéia de número finalmente tornou-se suficientemente ampla e vívida para que se sentisse a necessidade de exprimir a propriedade de algum modo, presumivelmente a princípio somente na linguagem de sinais. Os dedos de uma mão podem facilmente ser usados para indicar um conjunto de dois, três, quatro ou cinco objetos, não sendo o número 1 geralmente reconhecido inicialmente como um verdadeiro número. Usando os dedos das duas mãos podem ser representadas coleções contendo até dez elementos; combinando dedos das mãos e dos pés pode-se ir até vinte. Quando os dedos humanos eram inadequados podiam ser usados montes de pedras para representar uma correspondência com elementos de um outro conjunto. Quando o homem primitivo usava tal método de representação, ele frequentemente amontoava as pedras em grupos de cinco, pois os quíntuplos lhe eram familiares por observação da mão e pé humanos. Como Aristóteles observou há muito tempo, o uso hoje difundido do sistema decimal é apenas o resultado do acidente anatômico de que quase todos nós nascemos com dez dedos nas mãos e nos pés. (BOYER, 1996, p. 3)

 

Contudo, a Matemática desenvolveu-se e não se limitou somente em resolver questões de necessidades práticas de indivíduos e comunidades (como o caso da contagem), mas passou a ser uma área do conhecimento que exigia muitas abstrações. Elas se tornaram necessárias para o entendimento de objetos e, especialmente na álgebra, para a prova de uma afirmação dentro de uma base de conceitos pré-estabelecidos (axiomas). Em geometria analítica, um vetor em pode facilmente ser representado de forma algébrica por  ou, na sua forma gráfica, no plano xyz como indica a flecha em vermelho na figura abaixo:

Figura 1 – Representação geométrica de um vetor em R3

Fonte: O autor, 2020.

Pensando agora em  (com n natural maior que 3) a representação gráfica se torna impossível. Assim, são necessárias formas distintas de representar um vetor. Mas afinal: o que é o objeto vetor? Ao buscar uma resposta matemática conceitualmente correta nos livros técnicos, basicamente encontrar-se-á que vetor, nada mais é que, um conjunto de segmentos orientados que possui módulo, direção e sentido. Analisando esta definição, observa-se que a expressão “conjunto” não está totalmente explícita nas formas apresentadas acima (algébrica e gráfica). Isto leva a conclusão de que objetos matemáticos, em geral, são apenas representados. Neste âmbito, esse artigo discutirá, numa perspectiva epistemológica, alguns aspectos referentes as representações dos objetos matemáticos trazendo para discussão as concepções da semiótica de Charles Sanders Peirce e os Registros de Representação Semiótica de Raymond Duval como norteadores para a apreensão destes objetos. Por fim, a partir de uma análise epistemológica, trará o entendimento de Duval sobre a aprendizagem em Matemática a partir de sua teoria. Para isso será usado o conceito de função polinomial do primeiro grau e serão exploradas suas variáveis simbólicas significativas, seus respectivos valores e, consequentemente, a importância da interpretação global deste objeto matemático no processo de conversão entre diferentes registros.

1.  A concepção de Matemática: Empirismo x Racionalismo e a necessidade das representações dos objetos matemáticos

 

Johannes Hessen, em seu livro intitulado Teoria do Conhecimento, faz um apanhado das visões que definem a relação entre sujeito e objeto e, consequentemente, como se estrutura e se desenvolve o conhecimento a partir destas concepções. Dentre essas visões, o autor aborda o Racionalismo e Empirismo. Segundo o autor:

 

Chama-se de racionalismo (de ratio, razão) o ponto de vista epistemológico que enxerga no pensamento, na razão, a principal fonte do conhecimento humano. Segundo o racionalismo, um conhecimento só merece realmente esse nome se for necessário e tiver validade universal. (HESSEN, 1999, p. 48).

 

Contextualizando essa percepção de Hessen dentro dos campos de estudos da Matemática, é razoável assegurar que uma afirmação matemática somente é verdadeira se for possível estruturar uma prova lógica-dedutiva a partir de uma estrutura teórica previamente estabelecida (axiomas). Motivo pelo qual, o autor afirma que o saber matemático é uma forma de interpretação racionalista do conhecimento. Cita ainda a geometria que possui sua origem em axiomas e que sua estrutura é independente de qualquer tipo de experiência entre o sujeito e objeto (HESSEN, 1999, p. 49).

No empirismo, todavia “a razão não possui nenhum patrimônio apriorístico. A consciência cognoscente não retira seus conteúdos da razão, mas exclusivamente da experiência” (HESSEN, 1999, p. 55). Essa visão pode ser geradora de erros em uma afirmação Matemática. Para ilustrar, considere a expressão algébrica n2+n+41 com n∈Z+.  Observe o que ocorre ao atribuir valores para a variável n:

 

Quadro 1 – Resultados obtidos na expressão atribuindo valores para “n”

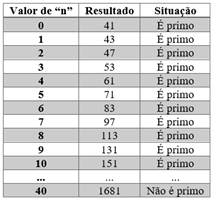
Fonte: O autor, 2020

No quadro 1, podemos observar que até n = 39 os valores obtidos a partir da expressão supracitada resultarão num número primo. Do ponto de vista empirista é possível que essa expressão possa representar somente números primos maiores ou iguais a 41 dado que, para 40 valores inteiros não-negativos de n (variando 0 a 39), resultam num valor primo. Esta situação retrata como a experimentação na Matemática pode chegar a conclusões equivocadas. Para um racionalista, a tese sobre esta expressão só poderia ser aceita a partir de uma prova direta, ou refutada com uma contraprova (contraexemplo). O contraexemplo já está na própria tabela. O leitor então poderia se questionar que até o racionalista poderia cair na tentação de aceitar esta tese, pois não teria o trabalho de verificar até n = 40. Mas há outros caminhos possíveis que não necessariamente necessitam atribuir valores de “n” ao acaso. Daí a importância das representações em Matemática. Pode-se pensar numa contraprova a partir da seguinte ideia: é possível que para algum n inteiro não-negativo podemos encontrar um valor resultante que não seja primo para a expressão n2+n+41? Considerando n par, pode-se escrever n = 2k. Substituindo na expressão obtêm-se 4k2+2k+41=2.2k2+k+41. Note que as expressões 2.2k2+k é um número par, pois há o fator 2 nesta multiplicação. Somando um número par a um valor ímpar, neste caso 41, tem-se como resultado um número ímpar para a expressão. Considerando n ímpar agora, é possível denotá-lo por n = 2k + 1.  Chegar-se-á à expressão 22k2+3k+43. Observe esta expressão é um número ímpar pelo mesmo motivo já exposto. Assim, a conclusão que é que para qualquer valor de n, tal que n∈Z+, tem-se um valor ímpar. Mas será que todo número ímpar obtido dessa expressão representa um primo? Considere agora a seguinte situação:  n2+n+41=k' sendo k'[Imagem local removida] um número ímpar. Desta forma, tem-se:n2+n+41-k'=0. Usando a técnica do completamento de quadrados chega-se a seguinte expressão: n+12=k'-1634.  Admitindo que essa equação possua raízes reais, deve-se admitir que k'-1634≥0, ou seja, k'≥40,75. É importante lembrar que por hipótese, o k' é um número ímpar. É sugestivo então que se tome n=41 na expressão n2+n+41.  Fica evidente agora que nem todo ímpar resultante da expressão é primo. Note que para n=41 o valor obtido na expressão é múltiplo de 41. Neste caso, o valor atribuído para n não foi obtido de forma aleatória, mas sim porque chega-se a uma conclusão para k'[Imagem local removida] que induz a tentativa de n para um valor inteiro maior que 40,75, neste caso, 41. A simbologia e representações implementadas no desenvolvimento da contraprova chegaram a uma conclusão que refutou a ideia inicial acerca da expressão sempre fornecer primos maiores ou iguais a 41. 

A partir desta exemplificação nota-se que para realizar provas em Matemática são necessárias formas de representar objetos assim como manipulá-los. Nas próximas seções buscar-se-á entender a estrutura das representações dos objetos Matemática e como é possível ter acesso a eles.

 

2.  Forma de acesso aos objetos matemáticos X objetos de outras ciências

 

O acesso aos objetos matemáticos não ocorre da mesma forma como em outras áreas do conhecimento. Se pensarmos, por exemplo, na Biologia, pode-se ter uma percepção concreta dos objetos para estudá-los, ou seja, a partir de uma percepção físico-sensorial é possível observar a folha de uma planta, ou uma organela num microscópio. É plausível indagar então de que forma é possível estudar entes matemáticos a partir de uma percepção direta (físico-sensorial). Duval (2011) entende que não há meios físicos de conceber objetos matemáticos e que, para serem compreendidos, são necessárias as representações. Por esse motivo, o entendimento desta área do conhecimento difere-se das outras. “[...] existem na Matemática, como aliás em qualquer outro ramo da Ciência, << problemas próprios >>, nascidos exclusivamente delas e só acessíveis aos seus especialistas” (CARAÇA, 1979, p. 293). Estes problemas, contudo, necessitam de uma simbologia própria, primeiramente para serem estruturados, posteriormente desenvolvidos e finalmente resolvidos. Neste sentido, Duval (2011, p. 24) percebeu que “A emergência da álgebra como criação de um simbolismo, que vai constituir << a língua dos cálculos >> segundo a célebre fórmula de Condillac[1], marca uma nova etapa no desenvolvimento do pensamento matemático”. Não obstante, o desenvolvimento da Matemática não se limitou somente a simbologia encontrada na álgebra. As conexões entre representações gráficas e representações algébricas (equações) foram fundamentais para a apreensão do objeto (DUVAL, 2011). Isto porque cada forma de representação do objeto é capaz de fornecer informações distintas sobre ele, assim obtém-se mais elementos para evidenciar propriedades dos entes matemáticos que se buscam compreender. Duval (2011) aponta ainda que o desenvolvimento do Cálculo Infinitesimal por Newton e Leibniz só foi possível pelo fato das representações semióticas darem acesso indireto e ilimitado aos entes matemáticos e consequentemente ao desenvolvimento e aperfeiçoamento do que se chama hoje de Cálculo Diferencial e Integral.

 

3.  Os signos de Peirce e as Representações Semióticas de Duval

 

Charles Sanders Peirce foi um matemático e filósofo americano que viveu entre os anos de 1839 e 1914. Seus estudos foram de grande contribuição para a Semiótica que, mais tarde, influenciou Raymond Duval na construção de sua Teoria dos Registros de Representação Semiótica (TRRS). Para Peirce (2000, p. 46),

 

Um signo, ou representàmen, é aquilo que, sob certo aspecto ou modo, representa algo para alguém. Dirige-se a alguém, isto é, cria, na mente dessa pessoa, um signo equivalente, ou talvez um signo mais desenvolvido. Ao signo assim criado denomino interpretante do primeiro signo. O signo representa alguma coisa, seu objeto.

 

A partir dessa ideia, é razoável entender o termo “signo” como um elemento de representação do objeto, mas não o próprio objeto. Este conceito remete ao que foi citado na introdução sobre as formas distintas de representar um vetor (forma geométrica, algébrica[2]), mas que não são o vetor. Todavia, sob certos aspectos, expressam como esse objeto matemático se comporta ou se caracteriza. Na geometria analítica e álgebra linear, por exemplo, essas diferentes formas representativas do vetor são usadas em situações distintas. A forma algébrica expressa qual a dimensão do espaço vetorial considerado e a localização da extremidade de um representante desse vetor na base canônica; a forma geométrica por sua vez é capaz de expressar o módulo (tamanho), direção e sentido desse vetor até a terceira dimensão.

Peirce apresenta em sua obra a segunda tricotomia dos signos, que podem ser classificados: Ícone, Índice ou Símbolo:

 

[...] Ícone é um signo que se refere ao Objeto que denota apenas em virtude de seus caracteres próprios, caracteres que ele igualmente possui quer um tal Objeto realmente exista ou não.

[...] Índice é um signo que se refere ao Objeto que denota em virtude de ser realmente afetado por esse Objeto. Portanto, não pode ser um Qualissigno, uma vez que as qualidades são o que são independentemente de qualquer outra coisa. Na medida em que o índice é afetado pelo Objeto, tem ele necessariamente alguma Qualidade em comum com o Objeto, e é com respeito a estas qualidades que ele se refere ao Objeto.

[...] Símbolo é um signo que se refere ao Objeto que denota em virtude de uma lei, normalmente uma associação de idéias gerais que opera no sentido de fazer com que o Símbolo seja interpretado como se referindo aquele Objeto. (PEIRCE, 2000, p. 52)

 

 Há, todavia, dez tricotomias dos signos, porém nesta discussão será apresentada somente a segunda, pois esta é a discutida por Duval, segundo Novak e Brandt (2018, p. 6). Assim, para uma análise epistemológica mais objetiva sobre as representações de objetos matemáticos, limitar-se-á a elementos relevantes de cada autor para a discussão que se pretende fazer aqui. 

Para elucidar a classificação dos signos feitos por Pierce, considere uma ilustração feita por um pintor de um cenário natural. Esta obra de arte pode ser considerada como um ícone (similaridades com o objeto). Pegadas profundas e grandes num terreno argiloso podem indicar um animal de grande porte, assim pegadas representam um índice (causa → consequência). O desenho de uma caveira sobreposto a duas tíbias cruzadas, representa um tipo de veneno, neste caso o primeiro representa um símbolo (ideia sobre o objeto). Duval (2011, p. 33) ilustra a ideia de Peirce na aquisição de conhecimentos matemáticos:

Figura 2 – Partição tricotômica das representações em função de sua relação com o objeto que elas evocam

Fonte: Duval, 2011.

 

Essa tricotomia de Peirce, “se limita à propriedade comum às representações e aos signos (“se colocar no lugar de...”), e ela ignora a propriedade específica dos signos (sua relação com o objeto é uma relação de referência e não de efeito e causa).” (DUVAL, 2011, p. 34)

Na Matemática surge a grande importância de representar os objetos, pois estes entes são abstratos, ou seja, puramente conceituais. Além disso, ela é “o domínio do conhecimento no qual existe quase sempre, se não sempre, prioridade das representações sobre os objetos do conhecimento” (DUVAL, 2011, p. 34). Duval estuda a relevância dos diferentes Registros de Representação Semiótica (RRS), justamente pelo fato de que a apreensão de um objeto matemático, segundo ele, está pautada na atividade cognitiva de conversão entre esses registros que muitas vezes são confundidos com os próprios objetos. Ele usa o termo representações semióticas e não signos, pois entende que a primeira terminologia apresenta dois atributos não presentes na segunda. De acordo com ele, as representações semióticas

 

[...] têm uma organização interna que varia de um tipo de representação semiótica para outra. A organização de uma frase simples não é o mesmo de uma equação. A organização interna de uma representação gráfica não é a de uma figura geométrica ou de um esquema etc. Depois, e não importa qual representação semiótica, existem várias maneiras de distinguir as unidades de sentido ou os níveis de organização (DUVAL, 2011, p. 37, grifo do autor).

 

Atualmente, Raymond Duval é um pesquisador francês, professor emérito da Université du Littoral Côte d’Opale e psicólogo de formação. O estudioso entende que não há como falar sobre fenômenos relativos ao conhecimento sem incluir as representações. Em sua obra intitulada Semiosis y Pensamiento Humano: Registros Semióticos y Aprendizajes Intelectuales[3] (2004), o autor faz um apanhado histórico acerca do estudo das representações na aquisição de conhecimentos: entre 1924 e 1926 com Piaget e as representações na mente das crianças; entre 1955 e 1960, as representações computacionais e a interpretação dos sistemas a partir de informações recebidas; por fim, a partir de 1985, as representações semióticas no processo de aprendizagem em Matemática.

A partir das ideias e críticas relacionadas a Semiótica de Peirce, Duval preocupou-se em entender a distinção entre objeto e a representação de um objeto matemático, e de que forma se dá a apreensão destes entes do ponto de vista cognitivo, não deixando de lado a questão epistemológica. Neste sentindo, Duval (2011, p. 15, grifo do autor) reforça:

 

Precisamos primeiro nos interrogar sobre o que é o conhecimento matemático e sobre o que pode ter de diferente em relação aos outros tipos de conhecimento. Essas questões são ao mesmo tempo de ordem epistemológica e cognitiva, sem que possamos separar esses dois aspectos. A análise do conhecimento não deve considerar apenas a natureza dos objetos estudados, mas igualmente a forma como os objetos nos são apresentados ou como podemos ter acesso a eles por nós mesmos.

 

No que diz respeito a forma de como os objetos são apresentados, Duval refere-se as distintas representações de um objeto e consequentemente as informações que cada uma delas fornece. Segundo Duval (2011, p. 18), “a diversidade de representação de um mesmo objeto tem origem na variedade dos sistemas físicos ou semióticos que permitem produzir as representações”. Na Matemática, em particular, ele entende que somente é possível ter acesso aos objetos a partir de suas representações, fato este que o levou, previamente, a refletir sobre a distinção epistemológica entre objeto e representação para posteriormente analisar de que forma se aprende em Matemática.

 

4.  Os Registros de Representações Semióticas (RRS) de Duval e a aprendizagem em matemática

 

  A expressão “o triplo de um número somado com dois” é uma representação de um objeto matemático. Este mesmo objeto pode ser representado pela expressão y=3x+2 ou ainda por uma reta no plano cartesiano. De acordo o esquema abaixo é possível classificar cada uma dessas representações e qual objeto matemático elas designam:

 

Quadro 2 – Diferentes RRS de uma função polinomial do primeiro grau

Língua natural	Expressão algébrica	Gráfico (reta)	Objeto matemático
o triplo de um número somado com dois	y=3x+2		Função polinomial de primeiro grau

Fonte: O autor, 2021.

Segundo Paiva (2010), uma relação entre dois conjuntos A e B não vazios é uma função se, e somente se, todo elemento de A está associado a um único elemento de B por uma regra. Esse ente matemático não é tocável, isto é, não é concreto – é um conceito. Esta definição, de acordo com o quadro 2, têm algumas representações. Para Duval, quanto mais variabilidade das representações de um objeto, mais informações e facilidade de acesso a ele serão obtidas. Consequentemente, a distinção entre representação do objeto e o próprio objeto será mais evidente.

 

As representações diferentes de um mesmo objeto, não tem evidentemente o mesmo conteúdo. Cada conteúdo é comandado por um sistema pelo qual a representação foi produzida. Daí a consequência de que cada representação não apresenta as mesmas propriedades ou as mesmas características do objeto. Nenhum sistema de representação pode produzir uma representação cujo conteúdo seja completo e adequado ao objeto representado. (DUVAL, 1999, p. 18 apud MORETTI, 2002, p. 347)

 

A partir destas discussões é possível pensar nos Registros de Representação Semiótica na perspectiva do aprendizado em Matemática. Tendo em vista os aspectos epistemológicos discutidos até aqui, buscar-se-á entender, de forma suscinta, como se dá o processo cognitivo da apreensão de um objeto matemático a partir da Teoria dos Registros de Representação Semiótica de Raymond Duval. É fundamental ressaltar que essa teoria está amparada nas questões epistemológicas relacionadas aos objetos e suas formas de representá-los.

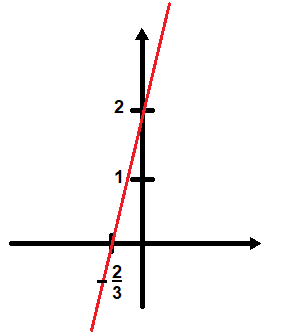
As representações apresentadas no quadro 2 fornecem dados distintos do objeto a que se refere. A língua natural é capaz de expressar quais operações devem ser realizadas com um número qualquer e o resultado obtido após essas operações. Porém, essa forma é bastante limitada para o entendimento global do objeto função. Na expressão algébrica é sabido que o coeficiente de x (neste caso 3) está relacionado com o fato da função ser crescente, por ser um valor positivo. Isto é, se for atribuído na expressão um x2>x1, será obtido um y2>y1. No gráfico, é possível enxergar a forma geométrica (reta) formada por todos os pares ordenados associados a função y. Também é possível ver que a reta intercepta o eixo vertical no ponto (0; 2), fato este que está diretamente relacionado com o termo independente da expressão algébrica (neste caso 2). Note que a representação algébrica fornece muito mais elementos para a apropriação do objeto. Duval (2015, p. 53-54) destaca diferenças significativas entre a simbologia e a linguagem natural:

 

Existem duas diferenças decisivas que fazem das escritas simbólicas um registro diferente do da língua. Primeiro, a organização das letras, dos números e dos símbolos de relação em expressões que são ou os termos, ou uma equação, é puramente operatória: ela depende de operações do tipo aritmética, conjuntista, ou lógica como a negação. Isso é radicalmente diferente da organização das palavras em sintagmas[4] ou em frases: ela depende da função das palavras, função invariável (artigo, nome, verbo, preposição). [...] Em seguida, os tratamentos que podemos efetuar com base em frases ou em proposições para desenvolver um raciocínio, uma explicação ou uma descrição, e aqueles que podemos efetuar com base em equações para executar um cálculo não são os mesmos. A álgebra permite a generalização da operação semiótica de substituição.

 

Apesar de Duval visualizar elementos mais relevantes na escrita simbólica, sua teoria entende que “A compreensão (integral) de um conteúdo conceitual repousa sobre a coordenação de ao menos dois registros de representação e esta coordenação manifesta-se pela rapidez e espontaneidade da atividade cognitiva de conversão”[5] (DUVAL, 1993, p. 51 apud MORETTI, 2002, p. 349). A conversão é a ação de mudar de uma representação semiótica para outra. Contudo, esta ação pode ser custosa ou não para o aprendiz, do ponto de vista cognitivo. Se há facilidade em realizar essa conversão, diz-se que há congruência semântica entre os registros e consequentemente uma maior facilidade do aprendiz reconhecer o objeto (HILLESHEIM; MORETTI, 2013). Percebe-se aqui que o reconhecimento do objeto e a distinção entre suas diferentes formas de representação (discussão epistemológica) tem um impacto direto no entendimento de um conceito (objeto) matemático.

Num contexto mais geral, sabe-se que uma função polinomial do primeiro grau é denotada pela expressão y = ax+b com a e b números reais. Os números a e b impactam diretamente na forma como o gráfico dessa função (neste caso, a reta) vai estar disposta no plano cartesiano. Dessa maneira, esses números são caracterizados como unidades significativas desta expressão. De acordo com Duval,

 

Em uma expressão algébrica, cada símbolo corresponde geralmente a uma   unidade significativa. Existe, no entanto, unidades significativas em que os símbolos são omitidos: o coeficiente 1, o caráter positivo dos coeficientes maiores do que zero. Deste modo, não se escreve y = +1x, em contrapartida, escreve-se y = –2x.  O lembrete desta trivialidade é importante uma vez que se trata de fazer corresponder variáveis visuais pertinentes do gráfico com unidades significativas da expressão algébrica. (DUVAL, 2012, p. 100).

 

A partir do exposto, Duval ressalta a importância de se estabelecer o que cada unidade simbólica significativa afeta nas variáveis visuais, (elementos do gráfico) quando são modificadas. Isso se faz fundamental no processo de conversão do registro de representação algébrico para o gráfico. Note que, dada uma função afim, é muito simples descrever o gráfico a partir de uma abordagem ponto a ponto, isto é,

 

Em referência aos dois eixos graduados, um par de números permite identificar um ponto (e, inversamente, um ponto se traduz por um par de números). Este modo associativo limita-se a alguns valores particulares e aos pontos marcados no plano referencial. Esta abordagem favorece quando se quer TRAÇAR o gráfico correspondente de uma equação do primeiro grau. (DUVAL, 2012, p. 98).

 

Contudo, ao tentar converter o registro gráfico para o algébrico, a estratégia ponto a ponto torna-se inviável, pois o uso desta abordagem “é totalmente inoperante uma vez que tira a atenção das variáveis visuais. [Esta prática] não favorece a abordagem de interpretação global [...]” (DUVAL, 2012, p. 99).

Neste sentido, Duval (2012) apresenta o seguinte quadro referente ao estudo das funções polinomiais do primeiro grau:

Quadro 3 - Valores e variáveis visuais para y = ax + b no plano cartesiano.

Identificadas as variáveis visuais, seus valores e as unidades simbólicas correspondentes, a partir deste quadro construído por Duval, fica evidente que, no caso em que a função é afim, o coeficiente angular (número real a) e o coeficiente linear (número real b) são os elementos mais significativos para sua análise. Nesta situação é possível compreender que, realizar a conversão da forma gráfica para a forma algébrica (forma simbólica), é muito mais custoso do que o processo inverso, visto que no primeiro caso é fundamental reconhecer as variáveis visuais e relacioná-las entre si, necessitando assim da interpretação global do objeto (DUVAL, 2012, p. 102).

É importante destacar que essa ideia é possível ser aplica para uma função polinomial do segundo grau cuja forma algébrica é f(x) = ax²+bx+c, porém essa abordagem é muito mais complexa para a função quadrática. Neste caso, são necessárias ferramentas mais sofisticadas como o cálculo diferencial e integral para minimizar o trabalho. Porém, este é um tema que não é abordado no ensino básico. Assim, surge o seguinte questionamento: qual a abordagem que se deve dar a esse objeto para que a relação entre variáveis visuais de representação e unidades significativa da escrita simbólica continue sendo evidenciada?  Nesta perspectiva Moretti (2003, p. 152, grifo do autor) endossa:

 

[...] é preciso conhecer de antemão a forma da curva, para depois, então, poder esboçá-la segundo [...] [o procedimento de interpretação global das propriedades figurais]. No entanto, acreditamos que o uso de uma noção bastante simples como a translação pode contribuir para que o esboço da curva mantenha-se bastante próximo do procedimento que permite estabelecer correspondência entre gráfico e expressão algébrica. Essa transformação possibilita que se percebam mudanças tanto na posição da curva quanto na expressão algébrica correspondente.

 

No trabalho supracitado, com exemplos não genéricos, o autor faz o tratamento da expressão y = ax² + bx + c para sua expressão equivalente canônica y+b²-4ac4a=ax+b2a2.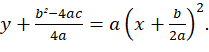  Esta expressão, apesar de aparentemente ser mais complexa, quando são atribuídos valores numéricos aos coeficientes a, b e c, ela se torna mais simplificada. Além disso, fornece informações acerca do deslocamento da curva com relação ao eixo horizontal e vertical. Neste caso, se a expressão b²-4ac4a(*) 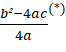 resulta num valor positiva, tem-se um deslocamento vertical para baixo; caso contrário, será para cima. De forma análoga, se a expressão b2a(**) 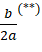 gera um número positivo, temos um deslocamento horizonta para a esquerda; caso contrário, será para a direita. Ademais, pensando numa translação de uma parábola que possui vértice na origem, as expressões (*) e (**) estão diretamente relacionadas com as coordenadas do vértice. Neste caso, pode-se justificar as fórmulas do vértice que são apenas enunciadas nos materiais didáticos, muitas vezes sem nenhuma justificativa: -b2a;-b2-4ac4a=-b2a;-Δ4a 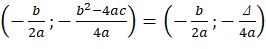. Fica também simples justificar a mudança de sinal nas coordenadas do vértice, pelo fato de que a abcissa e a ordenada deste ponto são valores que, ao serem inseridos na forma canônica, zeram a expressão.

Apesar de Duval, predominantemente, trabalhar com temas do ensino fundamental é possível expandir sua teoria para todos os campos da Matemática. Nesta seção foi apresentado o objeto “função polinomial do primeiro grau” e “função polinomial do segundo grau”, mas é possível estabelecer a mesma linha teórica para o estudo da reta e parábola em geometria analítica. Neste caso ainda, teremos mais informações que a análise numa perspectiva do tema funções, visto que no caso da parábola, é necessário analisar os casos quem o eixo de simetria não é paralelo ao eixo horizontal. No caso, das retas, o único caso a se analisar seria aquela que é paralela ao eixo vertical, já que é o único caso que a reta não representa uma função afim.

Com essas abordagens, é possível verificar a versatilidade que a Matemática tem e as múltiplas formas de fazer uma análise mais sofisticadas dos objetos a partir do tratamento e conversões presente na TRRS de Duva.

De forma geral, os campos de estudo da Matemática tiveram sua origem a partir de problemas reais que necessitavam de uma solução prática. Contudo, ao longo da sua história e de seu desenvolvimento surgiram problemas de cunho abstrato que necessitavam se amparar em símbolos e representações, pois os objetos considerados passaram a ser mais complexos. Além disso, estes objetos não conseguiam ser acessados de forma física, fato este que levou a Matemática a se diferenciar de outras áreas do conhecimento. A álgebra, em particular, se destaca, pois ela é responsável por elementos significativos na modelagem de situações reais. As discussões de cunho epistemológico entre a representação do objeto e o próprio objeto levam hoje a estudos no campo dos processos cognitivos na aprendizagem em Matemática. Desta forma, falar dessa área de estudo sem se respaldar nas epistemes envolvidas nesse processo não faz sentido. Os obstáculos no processo de ensino da Matemática estão diretamente relacionados com as limitações do aprendiz em compreender as estruturas e informações que as representações fornecem, assim como, as dificuldades em realizar as conversões entre os registros de representação semiótica por parte dos aprendizes. Neste sentindo, buscou-se entender o conceito de “signos”, pensado por Peirce, e sua influência na origem da TRRS de Duval e, finalmente, a forma como essa teoria se aplica nos processos de aprendizagem em Matemática. As situações e ideias apresentadas neste texto (funções de primeiro e segundo graus) não são as únicas pelas quais se pode explorar as variáveis visuais e os elementos simbólicos significativos de um objeto matemático. Em tese, a Teoria de Registros de Representação Semiótica de Duval e sua Hipótese Fundamental de Aprendizagem estão pautadas nas estratégias de identificar esses elementos.